How to Deal with Outliers in Your Data 내용을 한글로 정리해 보았습니다.
아웃라이어란?
아웃라이어란 데이터 상의 다른 값들의 분포와 비교했을때 비정상적으로 떨어져있는 관측치이다.
하지만, 어느정도가 비정상적으로 떨어져 있는 데이터인지 말하기는 참 모호하다.
아웃라이어의 정도에도 차이가 있다. (Mild outliers / Extrem outliers)
아웃라이어는 실제로 가치있는 정보를 담고 있을 수도 있으며, 기록의 실수인한 무의미한 정보일 수도 있다.
따라서 아웃라이어의 실제 의미가 무엇인지에 대해 의문을 품고, 분석할 필요성이 있다.
데이터에서 어떻게 아웃라이어를 잡아낼 것인가
Data visualization은 데이터 분석에 있어서 필수적이다.
소통을 하기위해서도 중요하며, 데이터를 더 깊게 이해하기 위해서도 중요하다.
시각적으로 아웃라이어를 잡는 경우도 많다. 아웃라이어를 발견하기 위해 가장 많이쓰는 그래프는 boxplot과 scatterplot이다.
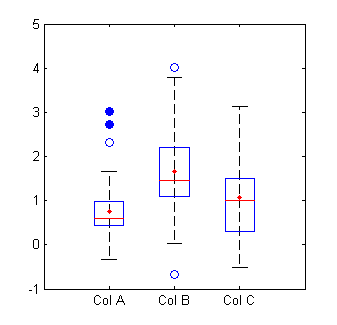
그래프를 보면 파란 점들이 아웃라이어라는 것을 알 수 있다.
파랗게 칠해져 있는 동그라미는 extreme outliers, 열려있는 동그라미는 mild outliers를 나타낸다.

IQR: Q3 - Q1
IQR을 이용한 방법은 Outlier Detection에서 쉽고, 자주 쓰이는 방법이다.
1.5이상이면 아웃라이어를 의심해봐야하고, 2IQR이상이면 극단치로 생각한다.
Scatter Plot
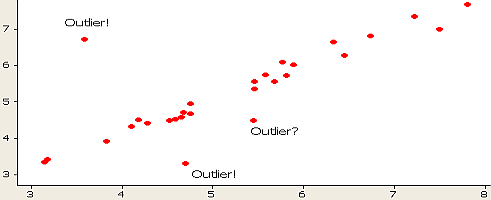
Histogram
아웃라이어를 어떻게 다룰 것인가
평균을 구할 때, 아웃라이어는 큰 영향을 미친다.
예를 들어서 100명의 고객이 백화점에 방문했는데
대부분 100달러 내외의 돈을 사용했고, 소수만이 200~1600달러 정도의 돈을 사용했다.
그런데 어떤 한 고객이 $29,000를 사용하면 자연히 평균값이 높아지게 된다.(한 사람당$2900꼴)
이러한 경우에는 양 극단 값을 제외하고 평균값을 구하는 것이 도움이 된다.

위의 R코드에서는 양 극단 10%를 제외한 평균값을 의미한다.
아웃라이어의 값 변경시키기
아웃라이어를 다루는데 있어서 가장 중요한 부분 중 하나는 아웃라이어를 발견했을 때 그 관측치를 계속해서 가지고 갈것인지, 제거할 것인지, 아니면 다른 값으로 변경시킬지에 있다.
단순히 아웃라이어를 제거하는 방법외에도 아래와 같이 아웃라이어의 값을 적절한 값(the trimmed minimuan and maximums)로 바꿔주는 방법도 있다.
Underlying Distribution 고려하기
Confidence Interval을 구하는 전통적이 접근법은 데이터가 Normal Distribution을 따른다고 가정한다.
하지만, 실제로 데이터가 정확하게 Normal Distribution을 따르는 경우는 많지 않다.
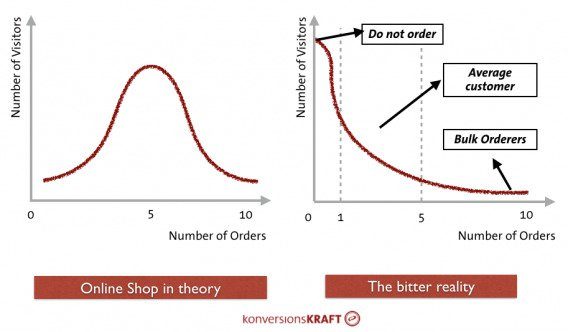
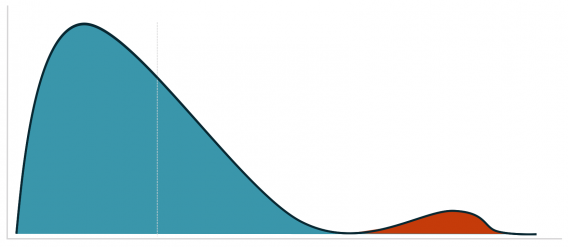
오른쪽에 보이는 그림은right-skwed distribution이라 불린다.
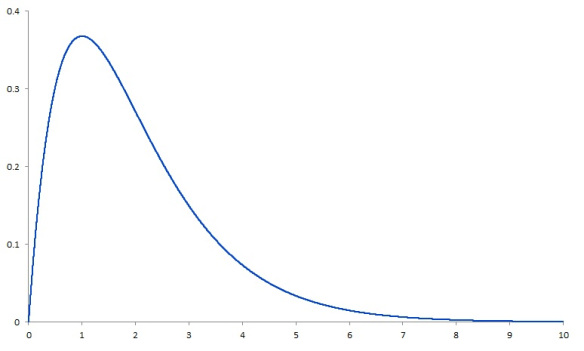
여기서 문제가 발생한다. 우리는 데이터가 정규분포를 따른다고 가정을 하고 분석을 하는데,
실제로는 right skewed한 데이터를 다루고 있다.
Confidence Interval이 신뢰할만하게 계살될 리가 없다.
이런 경우에는 t-test이외에 다른 메소드를 고려해볼만한 가치가 있다.
Mann-Whitney U-Test
Robust statistics
Bootstrapping
Mild Outliers 고려하기
데이터가 Normal distribution을 따르지 않는 경우에는 아웃라이어를 굉장히 많이 찾아내는 경향이 있다.
따라서 Outlier Detection에서 나온 아웃라이어라도 모두 버려서는 안된다.
아웃라이어들을 더 깊이 분석해보고 판단해야 한다.
'데이터분석' 카테고리의 다른 글
| 선형방정식과 행렬에 대해 알아봅시다. (0) | 2019.03.02 |
|---|---|
| 벡터공간에 대해서 알아보자 (벡터, 벡터공간, 선형방정식) (1) | 2019.02.20 |
| 선형대수 왜 공부해야할까? (1) | 2019.02.18 |


