선형대수 왜 공부할까?
요즘 KOCW 에서 이옥연 교수님이 강의하시는 선형대수학 강의를 듣고 있습니다. 현재 앞부분만 들었는데, '어떻게 이렇게 선형대수를 잘 가르치시나'하는 생각이 듭니다.. 대학교 1 학년 때 학교에서 선형대수를 들었고, KOCW 에서 이상화 교수님의 선형대수 강의를 들었지만 왜 선형대수, 벡터, 행렬 같은 것들을 배우는지 막막했는데 이 부분에 대한 명쾌하고 쉬운 답을 주십니다. 아래는 이옥연 교수님의 강의 링크입니다.
선형대수는 무엇을 공부하는 학문인가?
선형대수는 기본적으로 벡터공간을 공부하는 학문입니다. 벡터공간을 이해하기 위한 도구로서 행렬, 내적, 기저, 등을 배웁니다. 벡터공간에 대한 자세한 정의는 컨텐츠를 연재하면서 선형대수를 공부하면서 차차 알아가도록 하고, 이렇게 벡터공간을 배움으로써 무엇을 할 수 있느냐에 대해서 먼저 이야기를 해봅시다. 우리는 3 차원의 세계에 살고 있습니다. 시간이라는 개념을 포함해서 4 차원의 세계라고 표현하기도 하지만, 기본적으로 우리가 보고 느낄 수 있는 것은 3 차원입니다.
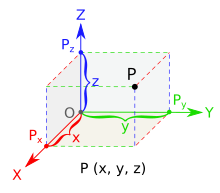
하지만, 우리가 보지 못한다고 해서 3 차원 이상의 공간이 존재하지 않을까요? 그렇다고는 할 수 없습니다. 우리가 보고 느끼지 못하여 알 수가 없을 뿐입니다. 요즘 뜨고 있는 인공지능, 머신러닝 같은 것들은 모두 3 차원 이상의 고차원 문제를 다루고 있습니다. 이렇게 우리가 보지 못하는 것들(우리가 보고 느끼고 있는 3 차원의 공간도)을 쉽게 이해하는데 도움을 주는 학문이 바로 선형대수학입니다. 스마트폰의 암호화 방식, 우리의 위치를 찾아내는 GPS, 최근 떠오르고 있는 머신러닝 모두 벡터공간이라는 개념을 사용합니다. 우리가 사용하고 있는 기술들 대부분이 벡터공간에 바탕을 두고 있습니다. 즉, 이러한 기술들을 생산하고 적용하는데 관심이 있다면 벡터공간을 반드시 이해해야 하고 선형대수를 공부해야만 합니다.
벡터 (Vector)
3 차원 이상의 문제를 쉽게 해결하기 위해 우리는 벡터라는 개념을 사용합니다. 보통 벡터는 크기와 방향을 가진 성분이라고 이야기합니다. 크기와 방향을 가졌기 때문에 아래와 같이 화살표로 표시할 수 있습니다.

하지만 실제로 벡터를 화살표로 표현하는 경우는 그렇게 많지 않습니다. 우선, 3 차원 이상의 공간에 대해서는 화살표로 표현하기가 어렵고, 화살표를 사용하지 않고 문제를 해결하는 경우가 편할 때가 많기 때문입니다. 위의 그래프에서 벡터 v 를 그림과 같이 화살표로 나타낼 수도 있고, (2, 3)처럼 수의 나열로 나타낼 수도 있습니다. 그리고 수를 나열하는 방식에는 두 가지가 있습니다.

행벡터

열벡터
첫 번째 그림처럼 수를 가로로 나열한 것을 행벡터라고 하고 두 번째 그림처럼 수를 세로로 나열한 것을 열벡터라고 합니다. 대부분의 경우 벡터라고 하면 열벡터를 지칭합니다.또한 나중에 자세히 다루겠지만, 이런 벡터들이 모여있는 공간을 벡터공간이라고 한다고 알아줍시다.
스칼라 (Scalar)
스칼라는 벡터와 다르게, 방향은 없고 크기만 존재하는 값을 의미합니다. 그리고 이러한 스칼라가 모여있는 집단을 스칼라체(Scalar field)라고 합니다. 여러 종류의 스칼라체가 있지만, 주로 실수(Real number)를 지칭합니다.
'데이터분석' 카테고리의 다른 글
| [요약] 데이터 아웃라이어 처리하기 (0) | 2019.03.02 |
|---|---|
| 선형방정식과 행렬에 대해 알아봅시다. (0) | 2019.03.02 |
| 벡터공간에 대해서 알아보자 (벡터, 벡터공간, 선형방정식) (1) | 2019.02.20 |


